Introduction
Backtracking is a search that find all possible solutions by enumerating on partial solutions. Backtracking can be done using DFS or BFS. Generally, DFS will be better than BFS because backtracking is used to enumerate many, many solutions. Since BFS requires storing each "level" of solutions and DFS requires storing each "height" of the solution, DFS will have a smaller memory footprint. In most backtracking problems, the "levels" of the solutions will be very large but the "height" will be small. Thus, DFS will be the preferred solution for most backtracking problems.
Backtracking is similar to recursion, but instead of generating all the solutions, we will generate each solution one by one. When backtracking, we only need to store the current solution in memory, whereas with normal recursion we need to store all the solutions into memory.
Since backtracking requires enumerating through all solutions, it is usually slow with runtimes such as O(n!) or O(2n).
![]()
General Solution
Base case:
When a solution has been generated
Reject:
Check if partial solution needs to be rejected
Recurrence:
Generate next partial solution thats growing to full solution
backtrack(solution):
if reject(solution)
stop
if base case
stop
backtrack( next_solution ) for next_solution
Initial:
backtrack( empty_solution)
List all sets
Given a set of numbers S of length N, output all subsets of S.
For example S=(1,2,3,4). The subsets of (1,2,3,4):
- ()
- (1), (2), (3), (4)
- (1,2), (1,3), (1,4), (2,3), (2,4), (3,4)
- (1,2,3), (1,2,4), (1,3,4), (2,3,4)
- (1,2,3,4)
We want to be able to enumerate all the subsets of S so we need to find a way to encode a subset of an array. We can use a binary number of length N to encode a subset of an array of length N. A one at position x will indicate that the xth number is in the set. For example, 1001 means the first and fourth is in the set so we have (1,4).
So above:
- () = 0000
- (1) = 1000
- (2) = 0100
- (3) = 0010
- (4) = 0001
- (1,2) = 1100
- (1,3) = 1010
- (1,4) = 1001
- (2,3) = 0110
- (2,4) = 0101
- (3,4) = 0011
- (1,2,3) = 1110
- (1,2,4) = 1101
- (1,3,4) = 1011
- (2,3,4) = 0111
- (1,2,3,4) = 1111
At each position, we either use or don't use the number in the set. We can enumerate through all possible encodings by starting with 0 or 1 and appending more 0's or 1's.
Recursive Method
Here is how we would solve this problem with recursion:
Start with [] Add 1 and 0 to the right of each binary number in the array Repeat until N [0,1] [00, 01, 10, 11] [000, 001, 010, 011, 100, 101, 110, 111] [0000, 0001, 0010, 0011, 0100, 0101, 0110, 0111, 1000, 1001, 1010, 1011, 1100, 1101, 1110, 1111] Let S be an array of N integers Let subsets(set, n) return an array of subsets of S from 1 to n Base case subsets(set, 0) = set Recurrence subsets(set,n) = subsets([sub+0 for sub in set] + [sub+1 for sub in set], n) Example: subsets([],4) subsets([0, 1], 3) subsets([00, 01, 10, 11], 2) subsets([000, 001, 010, 011, 100, 101, 110, 111], 1) subsets([0000, 0001, 0010, 0011, 0100, 0101, 0110, 0111, 1000, 1001, 1010, 1011, 1100, 1101, 1110, 1111], 0) = [0000, 0001, 0010, 0011, 0100, 0101, 0110, 0111, 1000, 1001, 1010, 1011, 1100, 1101, 1110, 1111]
However recursion uses a lot of memory to store all the solutions. Instead of building all the solutions, we can build each solution one by one and only store one solution at a time.
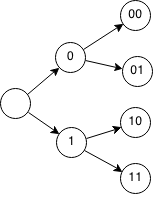
Formalization
Base case: subset(0, binary): print binary Recurrence: subset(n - 1, binary + '0') subset(n - 1, binary + '1') Example: subset(4,'') subset(3,'0') subset(3,'1') subset(2,'00') subset(2,'01') subset(2,'10') subset(2,'11') subset(1,'000') subset(1,'001') subset(1,'010') subset(1,'011') subset(1,'100') subset(1,'101') subset(1,'110') subset(1,'111') subset(0,'0000') subset(0,'0001') subset(0,'0010') subset(0,'0011') subset(0,'0100') subset(0,'0101') subset(0,'0110') subset(0,'0111') subset(0,'1000') subset(0,'1001') subset(0,'1010') subset(0,'1011') subset(0,'1100') subset(0,'1101') subset(0,'1110') subset(0,'1111')
Implementation
We can implement backtracking with recursion, but we pass in the same array instead of creating new ones. We only store one set at a time in the use[] array.
void subsets(int arr[], boolean use[], int i) {
int n = arr.length;
if (i >= n) {
for (int j = 0; j < n; j++) {
System.out.print(arr[i]);
}
System.out.println();
return;
}
use[i] = false;
subsets(arr, use, i + 1);
use[i] = true;
subsets(arr, use, i + 1);
}
// Example usage:
subsets([1, 2, 3, 4], [false, false, false], 0);
N Queen Problem
Find the number of ways to place N queens on a NxN board without any of them attacking each other. Queens can attack anything along its row, column or diagonal.
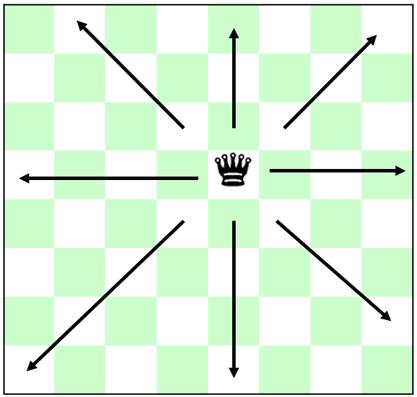
First we need to be able to encode a solution. There must be only one queen in each row, each column, each positive diagonal and each negative diagonal. We need a way to encode each row, column and diagonal to make it easy to check that they are all unique.
If we guarantee that all rows are unique and we have all columns filled, then we can guarantee that all the columns are unique as well.
To encode a diagonal we can use a clever equation to represent the diagonal. Notice that every positive diagonal has the same value for row+col.
d1 = row+column
N=6:
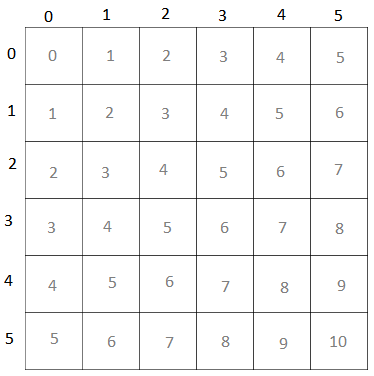
Every square with the same d1 is in the same diagonal ( / ). For example, on a 6x6 board: (0,2), (1,1), (2,0) all have d1 = 2 and are all along the same diagonal.
We can also see that every negative diagonal has the same value for (N-row)+column. The second diagonal can also be found using the following equation:
d2 = (N-row-1)+column
N=6:
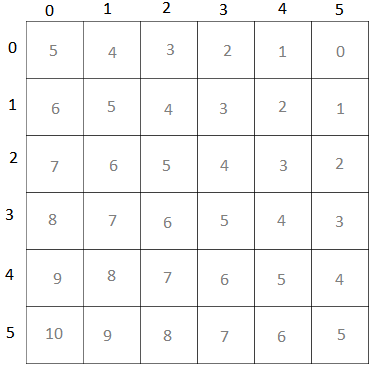
Everything with the same d2 will be on the same diagonal. For example, on a 6x6 board, (0,0),(1,1),(2,2) have d2 = 5 and are all along the same diagonal.
Now that we get can encode rows, columns, and diagonals, we can use it to make checking solutions more easy. We can keep sets that track with rows/columns/diagonals are currently filled and check our solution to make sure we do not have anything in the same row/column/diagonal.
We can place a queen in each row and make sure that each column / diagonals is unfilled.
Formalization
Let N be a NxN board where we want to place N queens Let queen(n,columns,d1,d2) be a placing of N queens across a board Base case queen(0, cols, d1, d2): print solution Reject solution reject(cols, d1, d2) = false if duplicates in cols or d1 or d2 reject(cols, d1, d2) = true otherwise Recurrence queen(row,cols,d1,d2) = queen(row-1,cols with col,d1 with row+col,d2 with N-row+col) for col from 1 to N Examples N=4 queen(4,[],[],[]) queen(3,[0],[3],[6]) queen(3,[1],[4],[5]) queen(3,[2],[5],[4]) queen(3,[3],[6],[3]) queen(2,[0,0],[3,2],[6,5]) x-- reject queen(2,[0,1],[3,3],[6,4]) x-- reject queen(2,[0,2],[3,4],[6,3]) queen(2,[0,3],[3,5],[6,2]) queen(2,[1,0],[4,2],[5,5]) x-- reject queen(2,[1,1],[4,3],[5,4]) x-- reject queen(2,[1,2],[4,4],[5,3]) x-- reject queen(2,[1,3],[4,5],[5,2]) queen(2,[2,0],[5,2],[4,5]) queen(2,[2,1],[5,3],[4,4]) x-- reject queen(2,[2,2],[5,4],[4,3]) x-- reject queen(2,[2,3],[5,5],[4,2]) x-- reject queen(2,[3,0],[6,2],[3,5]) queen(2,[3,1],[6,3],[3,4]) queen(2,[3,2],[6,4],[3,3]) x-- reject queen(2,[3,3],[6,5],[3,2]) x-- reject queen(1,[0,2,0],[3,4,1],[6,3,4]) x-- reject queen(1,[0,2,1],[3,4,2],[6,3,3]) x-- reject queen(1,[0,2,2],[3,4,3],[6,3,2]) x-- reject queen(1,[0,2,3],[3,4,4],[6,3,1]) x-- reject queen(1,[0,3,0],[3,5,1],[6,2,4]) x-- reject queen(1,[0,3,1],[3,5,2],[6,2,3]) queen(1,[0,3,2],[3,5,3],[6,2,2]) x-- reject queen(1,[0,3,3],[3,5,4],[6,2,1]) x-- reject queen(1,[1,3,0],[4,5,1],[5,2,4]) queen(1,[1,3,1],[4,5,2],[5,2,3]) x-- reject queen(1,[1,3,2],[4,5,3],[5,2,2]) x-- reject queen(1,[1,3,3],[4,5,4],[5,2,1]) x-- reject queen(1,[2,0,0],[5,2,1],[4,5,4]) x-- reject queen(1,[2,0,1],[5,2,2],[4,5,3]) x-- reject queen(1,[2,0,2],[5,2,3],[4,5,2]) x-- reject queen(1,[2,0,3],[5,2,4],[4,5,1]) queen(1,[3,0,0],[6,2,1],[3,5,4]) x-- reject queen(1,[3,0,1],[6,2,2],[3,5,3]) x-- reject queen(1,[3,0,2],[6,2,3],[3,5,2]) queen(1,[3,0,3],[6,2,4],[3,5,1]) x-- reject queen(1,[3,1,0],[6,3,1],[3,4,4]) x-- reject queen(1,[3,1,1],[6,3,2],[3,4,3]) x-- reject queen(1,[3,1,2],[6,3,3],[3,4,2]) x-- reject queen(1,[3,1,3],[6,3,4],[3,4,1]) x-- reject queen(0,[0,3,1,0],[3,5,2,0],[6,2,3,3]) x-- reject queen(0,[0,3,1,1],[3,5,2,1],[6,2,3,2]) x-- reject queen(0,[0,3,1,2],[3,5,2,2],[6,2,3,1]) x-- reject queen(0,[0,3,1,3],[3,5,2,3],[6,2,3,0]) x-- reject queen(0,[1,3,0,0],[4,5,1,0],[5,2,4,3]) x-- reject queen(0,[1,3,0,1],[4,5,1,1],[5,2,4,2]) x-- reject queen(0,[1,3,0,2],[4,5,1,2],[5,2,4,1]) SOLUTION queen(0,[1,3,0,3],[4,5,1,3],[5,2,4,0]) x-- reject queen(0,[2,0,3,0],[5,2,4,0],[4,5,1,3]) x-- reject queen(0,[2,0,3,1],[5,2,4,1],[4,5,1,2]) SOLUTION queen(0,[2,0,3,2],[5,2,4,2],[4,5,1,1]) x-- reject queen(0,[2,0,3,3],[5,2,4,3],[4,5,1,0]) x-- reject queen(0,[3,0,2,0],[6,2,3,0],[3,5,2,3]) x-- reject queen(0,[3,0,2,1],[6,2,3,1],[3,5,2,2]) x-- reject queen(0,[3,0,2,2],[6,2,3,2],[3,5,2,1]) x-- reject queen(0,[3,0,2,3],[6,2,3,3],[3,5,2,0]) x-- reject
Implementation
Here is a Java implementation of counting the number of ways to place 8 queens on board.
public int nqueen(int col, boolean row[], boolean d1[], boolean d2[]) {
int n = row.length;
// Base case if 8 queens are placed.
if (col >= n) {
return 1;
}
int sum = 0;
for (int r = 0; r < n; r++) {
// Check queen coordinates are valid.
if (!row[r] && !d1[r + col] && !d2[n - 1 - r + col]) {
// Mark rows and diagonals as filled.
row[r] = true;
d1[r + col] = true;
d2[n - 1 - r + col] = true;
// Backtrack positions.
sum += nqueen(col + 1, row, d1, d2);
// Clear rows and diagonals.
row[r] = false;
d1[r + col] = false;
d2[n - 1 - r + col] = false;
}
}
return sum;
}
int n = 8;
boolean[] row = new boolean[n];
boolean[] d1 = new boolean[2*n];
boolean[] d2 = new boolean[2*n];
for (int i = 0; i < n; i++) {
row[i] = false;
d1[i] = d2[i] = false;
}
nqueen(0, row, d1, d2);
Exercises
- Given a sequence of numbers, output all increasing subsequences.
- Given a NxN chessboard with certain squares that can have no pieces placed, output the number of configurations that can be made from rooks without attacking each other.
- Given a sudoku problem, output a solution for the grid if it exists. Note: this question is popular for technical interviews.
- Given a NxN magic square where you need to place the numbers from 1 to N2, find the number of ways to have every row, column and diagonal add to M.