Introduction
Data structures are different ways of storing data such that they optimize certain data operations such as retrieval and insertion. Although many of these data structures are already built into various languages, it is important to understand how they work. By understanding the implementations, we can have a sense of which data structure to use for different scenarios.
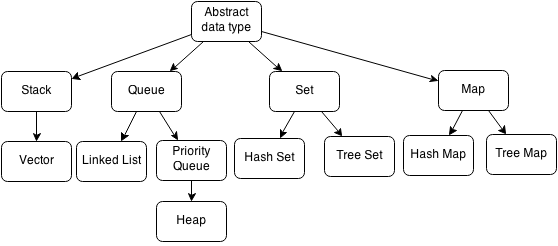
An abstract data type is a conceptual model for representing data. An abstract data type tells what it should do as opposed to how it should work. It will tell us what operations it should have but should not tell us how to implement them.
For example, a bottle should be able to hold water and allow us to drink from it. This tells us what it should do but we don't need to know how it works or how it is made. A plastic water bottle is an implementation of a bottle. It holds water in its interior and allows us to drink by unscrewing the cap and letting us pour water down our throat. A thermos is also an implementation of the bottle, it has a lid that can be popped open. and water can come from it. A thermos and plastic water bottle are different implementations as they are made differently and used differently, but they fundamentally do what a bottle is supposed to do: store liquid and provide a way to drink. A bottle in the abstract does not actually exist, but types of bottles do.
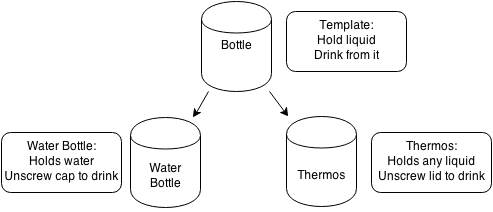
Some implementations of abstract data types are better than others for different purposes. For example, plastic water bottles are very cheap, whereas a thermos is more expensive. However, a thermos can hold hot water and keep it warm for a longer period of time. When selecting a data structure, we should pick one based on the efficiencies of data operations that we will do most often.
Stack
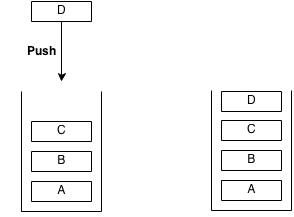
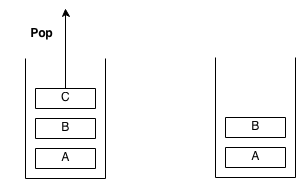
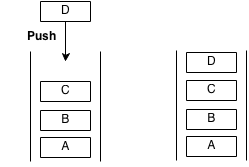
A stack is an abstract data type with the property that it can remove and insert elements following a FILO (First In Last Out) structure. The first element to be inserted must be the last element to be removed and the last element to be inserted must be the first element to be removed. Sometimes, removal is called "pop" and insertion is called "push".
Imagine a stack of plates at a buffet, the plates are taken from the top and are also replaced from the top. The first plate to go in will be the last plate to come out. The last plate to go in will be the first to come out. This structure is what a stack is.
Example of push:
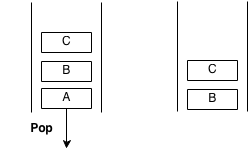
Example of pop:
Stacks are used to keep track of function calls in memory. Whenever a function is called, it is placed on the memory stack with its variables, and when it is returning a value, it is popped off the stack.
A stack is usually implemented as a vector.
Vector
A vector is a stack that is implemented as an array. It is very similar to an array, but it is more flexible in terms of size. Elements are added and removed only from the end of the array. When more elements are added to the vector and the vector is at full capacity, the vector resizes itself and reallocates for 2*N space. When using an vector we can keep adding elements and let the data structure handle all the memory allocation.
| Operation | Get | Push | Pop | Insert |
|---|---|---|---|---|
| Time Complexity | O(1) | O(1) | O(1) | O(n) |
Queue
A queue is an abstract data type with two functions, pop and push. Removal from the front is called "pop" or "dequeue". Insertion from the back is called "push" or "enqueue". A queue follows a First In First Out (FIFO) structure meaning the first element pushed should be the first element popped and the last element pushed should be the last element popped.
Imagine you are standing in line for a restaurant. Whoever is first in line will be served first and whoever is last in line will be served last. People can be served while more people join the line and the line may get very long because it takes a while to serve one person while more people join the queue. This is called a queue.
Queues are often used for buffer systems, such as a text message service. The messages that arrive at the server first are relayed first and the messages that arrive later are relayed later. If there are too many text messages in the system such that the rate texts are received overwhelm the number of texts that are sent the buffer may overflow and messages will get dropped. Most of the time this won't happen because the systems are designed to handle large loads, but if there were an emergency that caused everyone to start texting many texts could be dropped.
Example of push:
Example of pop:
Linked List
Prerequisites: Queue
A linked list is an implementation of a queue that uses a chain of pointers. Instead of storing all the data in a fixed set of memory, we can store each element by itself but have a pointer from each element to the next element. A pointer is something that holds the memory location of another object.
Imagine you were on a scavenger hunt with lots of treasure chests. You start with a clue to the first chest. Each chest contains a lot of gold (data) but it also contains a clue to the next treasure chest. To get to the fifth chest, you need to visit the first, second, third and fourth chest. This is essentially how a linked list works.
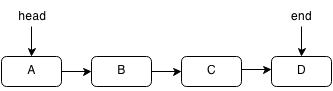
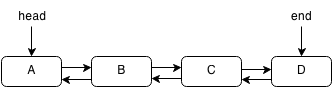
A linked list is similar to an array but it is different such that it is not stored in one block of data. Each element can be stored in a random place in memory but each element contains a pointer to the next element thus forming a chain of pointers. Think of a pointer as a clue to the next chest. Since the elements aren't in a block, accessing an element must be done by traversing the entire linked list by following each pointer to the next. However, this also allows insertion and deletion to be done more quickly. In a linked list the links only go forward and you cannot move backward. However, a doubly linked list is a linked list that has pointers going backwards as well as forwards.
| Operation | Get | Push | Delete | Insert |
|---|---|---|---|---|
| Time Complexity | O(n) | O(1) | O(1) | O(1) |
Trees
Trees are data structures that follow a hierarchy, each node has exactly one or zero parents and each node has children. Trees are recursive structures meaning that each child of a tree is also a tree. A tree within another tree is called a subtree.
A child is a node that is below another node.
A parent is a node that is above another node.
The element at the top of the tree with no parents is called a root. The node at the bottom of the tree with no children is called a leaf.
Each node can hold different kinds of information depending on the tree. A node can hold the children it has, the parent it has, a key associated with the node and a value associated with the node.
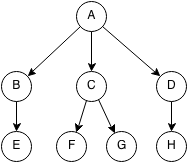
- A is the root of the tree and E,F,G,H are leaves.
- The parent of E is B.
- C,F,G is a subtree of the original tree.
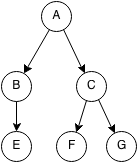
Binary Tree
A binary tree is a tree such that each node has at most 2 children.

Sets
Sets are abstract data structures which are able to store and keep track of unique values.
Imagine you have a grocery list that you use to keep tracking of things you need to buy. You want to make sure there are no duplicate items in the list, you can add items to the list and that you can remove items from your list. This structure is similar to what a set does.
Sets have three operations: insertion, deletion and a membership test. Insertion places an element into the set, deletion removes an element from the set and a membership test is checking whether an element exists within the set.
Hash Set
Prerequisites: Sets, Linked List
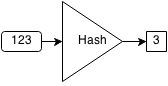
Hash sets are sets that use hashes to store elements. A hashing algorithm is an algorithm that takes an element and converts it to a chunk of a fixed size called a hash. For example, let our hashing algorithm be (x mod 10). So the hashes of 232, 217 and 19 are 2,7, and 9 respectively.
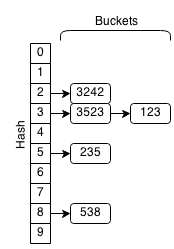
For every element in a hash set, the hash is computed and elements with the same hash are grouped together. This group of similar hashes is called a bucket and they are usually stored as linked lists.
If we want to check if an element already exists within the set, we first compute the hash of the element and then search through the bucket associated with the hash to see if the element is contained.
| Operation | Membership | Insertion | Deletion |
|---|---|---|---|
| Time Complexity | O(1) | O(1) | O(1) |
Tree Set
Prerequeisites: Sets, Binary Search Tree
A tree set is a set which stores the values in a binary search tree. To store elements in a tree set, they must be able to be sorted by a property. To insert an element, it is added to the binary tree. To delete an element, it is removed from the binary tree. To check for membership, we do a binary search for the element in the binary tree.
The advantage of tree sets is that they are maintained in a sorted order.
Tree Sets are implemented using binary search trees.
Maps
Prerequisites: Sets
A map is an abstract data type that stores key-value pairs.
Imagine you had a English dictionary. If you look up a word, you can find it's definition. For example if you looked up the word 'cat' in the English dictionary, you would look through the dictionary alphabetically until you found the word 'cat' and then you would look at the definition: 'a feline animal'. If you really wanted to, you could also add your own words into the dictionary and the definitions of your words. This type of structure is called a map.
Maps (also called dictionaries) are abstract data types that store pairs of key-values and can be used to look up values from the keys. The keys are like the words in an English dictionary and the definitions can be seen as the values. Maps are able to insert key-value pairs, retrieve values from keys, and delete key-value pairs.
Hash Map
Hash maps are maps that use hash sets to store pairs of key values. Implementations of hash maps are very similar to hash sets.
| Type | Get | Put | Deletion |
|---|---|---|---|
| Hash Map | O(1) | O(1) | O(1) |
Tree Map
Prerequisites: Maps, Binary Search Tree
A tree map is a map which stores the values in a binary search tree. To store elements in a tree map, they must be able to be sorted by a property. To insert an element, it is added to the binary tree. To delete an element, it is removed from the binary tree. To check for membership, we do a binary search for the element in the binary tree.
The advantage of tree maps is that they are maps maintained in a sorted order.

| Operation | Membership | Insertion | Deletion |
|---|---|---|---|
| Time Complexity | O(log n) | O(log n) | O(log n) |
Tree Maps are implemented using binary search trees. Since the implementation of a tree map is very similar to the implementation of a tree set, it will left as an exercise.
Priority Queue
A priority queue is a queue that takes elements which have the highest priority first. This is either the maximum or minimum property for all elements.
Consider a waiting list for lung transplants. The patients are given a score when they are placed on the waiting list based on whether they smoke, risk factors, age, expected time left, etc. When a lung is available, the patient with the highest score will receive the lung first. During this time, it is possible more patients could be added to the queue. The behaviour is similar to a queue but instead of the first person getting in the queue getting a lung first, the person with the highest score will get it. This means that if Sam, who has a score of 60, joins the queue after Bob, who has a score of 40, Sam will get the lung first even though Bob was in the queue before him.
A priority queue is an abstract data structure with two operations: push and pop. Push adds an element into the priority queue and pop removes the highest or lowest element.
A priority queue is usually implemented as a heap because it is the most efficient implementation.
Heap
Prerequisites: Queue
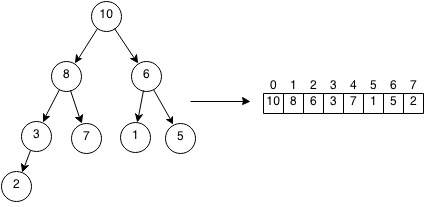
Heaps are data structures that can pop the maximum or minimum value or push a value very efficiently. Heaps are special binary trees which have the property that: the value of each node is greater than the values of all its children (a max heap) or the value of each node is less than the values of all its children (a min heap). Priority queue's are most efficiently implemented as heaps. This guarantees that the maximum or minimum element is the root node.
Heaps store their data level by level in a binary tree. This allows us to store heaps in an array. The root index is 0. For every node with index i, the left index can be found by using the formula 2*i+1 and the right index can be found by using the formula 2*i + 2. The parent of a node can be found by integer division as (i-1)/2.
root = 0 leftChild = index * 2 + 1 rightChild = index * 2 + 2 parent = (index - 1)/2
Indexes of a heap
Example Heap:
A heap has two operations: push and pop. Pushing an element into a heap adds it into the heap while ensuring that the properties of the heap still hold. Popping removes an element from the top of the heap and the heap needs to ensure that the properties of the heap still hold.
| Operation | Resize | Push | Pop | Heapify |
|---|---|---|---|---|
| Time Complexity | O(n) | O(log n) | O(log n) | O(n) |